HVDC Classic – Main Circuit Eq.

Huvudkretsekvationen för likspänning i HVDC-tillämpningar är ett utmärkt verktyg för att se vilka parametrar som påverkar bland annat Tap changer-kontrollen och hur förändringar i vinklar, ström och AC-spänning påverkar likspänningen och därmed effektöverföringen mellan två stationer. Som tidigare visats så ser en HVDC-station principiellt ut som på bilden nedan:

Man har alltså ett behov av att matematiskt kunna beskriva DC-spänningen beroende av omgivande faktorer. I avsnittet som skrevs förra veckan: Vi kontrollerar effekten! definierades den ideala så kallade ”No load voltage” till att vara:

Udi0 • cos(α)

Efter en kommentar kring denna ekvation så kan jag nämna att jag utgått ifrån ett kompendium, skrivet av Åke Ekström vid KTH, som behandlar högeffektelektronik där teorin kring högspänd likström hanteras väldigt ingående.  Där skrivs Udi0 som 3•√2/π • Uh, det vill säga huvudspänningen. Det man nu måste veta är att huvudspänningen för växelström är definierad som RMS-värdet av växelströmmen vilket är U Φ-Φ/√2. Jag har alltså förenklat ekvationens utseende.

Åter till att påpeka att uttrycket ovan är en ideal framställning av likspänningen. Det finns en hel del faktorer man måste beakta för att få en exakt ekvation, eller snarare en så pass exakt ekvation att den tillfredsställer tillämpningen. I alla fysiska material som leder ström finns det förluster som visar sig i form av värmeutveckling. För höga förluster kan skapa inte bara skada på utrustning utan även ekonomiska förluster (dessa tas dock inte i beaktande här av naturliga skäl).

Vart hittar vi förluster?

En stor del är förluster i transformatorerna som isolerar växelströmsnätet och likströmsnätet från varandra. Transformatorförluster visar sig främst som induktans, dvs. inducerade strömmar, i transformatorns lindningar. Denna förlust kan beräknas fram till en konstant term ,som beror på likströmmen, och betecknas generellt som dxN. Utöver dessa kan man anta att det finns resistiva förluster i material och även den kan beräknas till en konstant term beroende av likströmmens storlek. De resistiva förlusterna kan betecknas drN.

Utav detta får vi en sammanlagd term: (dxN + drN) • Id

Det kan vara värt att nämna att på grund av reaktanser som skapar dxN så får spänningen ett spänningsfall som även är kopplat till tyristorers fysiska begränsningar. Tillsammans skapar de ett så kallat överlapp i kommuteringen som enkelt innebär att två ventiler inom samma trepuls-grupp, under vissa perioder, leder samtidigt. En bild för den som är intresserad finns här, där den svarta linjen representerar likspänningen Ud.

Till sist har vi en term som representerar spänningsfall i tyristorventilerna som inte är relaterat till strömmen. Denna benämns oftast UT och motsvarar en 6-puls grupp, dvs. för en 12-puls grupp av ventiler så är parametern multiplicerad med 2; 2UT.

Slår man ihop alla dessa termer och skapar relativitet till nominella världen så får vi en komplett ekvation:

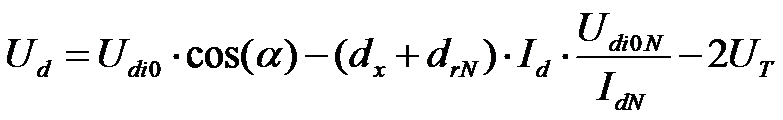
Denna ekvation är en HVDC-anläggnings huvudkretsekvation. Just den här ovan är refererad till likriktarstationen i en anläggning. För växelriktaren gäller en annan vinkel än tändvinkeln α (alpha), närmare bestämt en släckvinkel som ofta benämns γ (gamma). Dessutom är +/- tecken omvända.

Sammanfattningsvis kan man säga att det är en hel del parametrar att ta hänsyn till. Däremot finns det möjligheter att förenkla den ytterligare vid ”allmänna” beräkningar. drN och 2UT är så pass små procentenheter att de för det mesta kan bortses ifrån.

*******

Det finns att läsa mer kring ekvationerna för HVDC för den intresserade:

Hela kapitel 15 i boken ”Standard handbook for electrical Engineers” som finns via adlibris: LÄNK
Ovan nämnda bok finns också i fullt digital upplaga via Högskolan Västs databas dawsonera: LÄNK
Bilden som används i detta inlägg kommer från en powerpoint presentation kring HVDC Transmission från IEEE: LÄNK

Detta inlägg är en repris från min (inte längre aktiva) studentblogg.  Då jag spenderat de senaste tre dagarna med internkurser för nyanställda i HVDC Classic (en utbildning som jag hjälpte till att uppdatera) så tänkte jag det värt att åter lyfta fram denna text som beskriver basen, huvudkretsekvationen, för HVDC Classic.